best-time-to-buy-and-sell-stock

题目描述

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票一次），设计一个算法来计算你所能获取的最大利润。注意：你不能在买入股票前卖出股票。

题解

int maxProfit(vector<int>& prices) {
	int t1 = 0, t2 = 1;
	int vsize = prices.size();
	if (vsize <=1||(vsize==1&&prices[1]<prices[0]))return 0;
	int pro = prices[1] - prices[0];
	while (t2 < vsize)
	{
		if (prices[t2] > prices[t2 - 1])
		{
			for (int i = t1; i < t2; i++)
			{
				if (prices[t2] - prices[i] > pro)
				{
					t1 = i;
					pro = prices[t2] - prices[i];
				}
			}
		}
		t2++;
	}
	return pro;
}

题目描述

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

题解

既然可以买多次，那就把赚钱的时候都加起来就行了。

int maxProfit(vector<int>& prices) {
	int vsize = prices.size();
	if (vsize <= 1)return 0;
	int pro = 0;
	for (int i = 1; i < vsize; i++)
	{
		if (prices[i] - prices[i - 1]>0)
			pro += prices[i] - prices[i - 1];
	}
	return pro;
}

==题目描述==

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

==题解==

链接：https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii/solution/yi-ge-tong-yong-fang-fa-tuan-mie-6-dao-gu-piao-wen/

6 道股票买卖问题是有共性的，我们通过对第四题（限制最大交易次数为 k）的分析一道一道解决。因为第四题是一个最泛化的形式，其他的问题都是这个形式的简化。

第一题是只进行一次交易，相当于 k = 1；第二题是不限交易次数，相当于 k = +infinity（正无穷）；第三题是只进行 2 次交易，相当于 k = 2；剩下两道也是不限次数，但是加了交易「冷冻期」和「手续费」的额外条件，其实就是第二题的变种，都很容易处理。

利用「状态」进行穷举

具体到每一天，看看总共有几种可能的「状态」，再找出每个「状态」对应的「选择」。我们要穷举所有「状态」，穷举的目的是根据对应的「选择」更新状态。

for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 择优(选择1，选择2...)

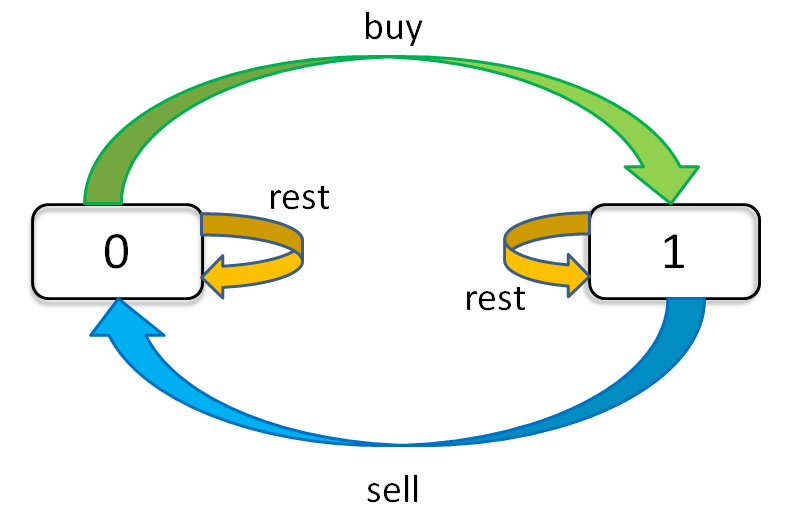
每天都有三种「选择」：买入、卖出、无操作，用 buy, sell, rest 表示这三种选择。 sell 必须在 buy 之后，那么 rest 操作还应该分两种状态，一种是 buy 之后的 rest（持有了股票），一种是 sell 之后的 rest（没有持有股票）。还有交易次数 k 的限制， buy 还只能在 k > 0 的前提下操作。

这个问题的「状态」有三个，第一个是天数，第二个是允许交易的最大次数，第三个是当前的持有状态（即之前说的 rest 的状态，我们不妨用 1 表示持有，0 表示没有持有）。然后我们用一个三维数组就可以装下这几种状态的全部组合：

dp[i][k][0 or 1]
0 <= i <= n-1, 1 <= k <= K
n 为天数，大 K 为最多交易数
此问题共 n × K × 2 种状态，全部穷举就能搞定。

for 0 <= i < n:
    for 1 <= k <= K:
        for s in {0, 1}:
            dp[i][k][s] = max(buy, sell, rest)

比如说 dp[3][2][1] 的含义就是：今天是第三天，我现在手上持有着股票，至今最多进行 2 次交易。再比如 dp[2][3][0] 的含义：今天是第二天，我现在手上没有持有股票，至今最多进行 3 次交易。

我们想求的最终答案是 dp[n - 1][K][0]，即最后一天，最多允许 K 次交易，最多获得多少利润。

状态转移图

状态转移方程：

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
              max(   选择 rest  ,           选择 sell      )

解释：今天我没有持有股票，有两种可能：
要么是我昨天就没有持有，然后今天选择 rest，所以我今天还是没有持有；
要么是我昨天持有股票，但是今天我 sell 了，所以我今天没有持有股票了。

dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
              max(   选择 rest  ,           选择 buy         )

解释：今天我持有着股票，有两种可能：
要么我昨天就持有着股票，然后今天选择 rest，所以我今天还持有着股票；
要么我昨天本没有持有，但今天我选择 buy，所以今天我就持有股票了。

注意 k 的限制，我们在选择 buy 的时候，把 k 减小了 1，很好理解吧，当然你也可以在 sell 的时候减 1，一样的。

定义 base case

dp[-1][k][0] = 0
解释：因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0 。
dp[-1][k][1] = -infinity
解释：还没开始的时候，是不可能持有股票的，用负无穷表示这种不可能。
dp[i][0][0] = 0
解释：因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0 。
dp[i][0][1] = -infinity
解释：不允许交易的情况下，是不可能持有股票的，用负无穷表示这种不可能。

新状态只和相邻的一个状态有关，其实不用整个 dp 数组，只需要一个变量储存相邻的那个状态就足够了，这样可以把空间复杂度降到 O(1):

具体实现

第一题，k = 1

dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], dp[i-1][0][0] - prices[i]) 
            = max(dp[i-1][1][1], -prices[i])
解释：k = 0 的 base case，所以 dp[i-1][0][0] = 0。

现在发现 k 都是 1，不会改变，即 k 对状态转移已经没有影响了。
可以进行进一步化简去掉所有 k：
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], -prices[i])

for (int i = 0; i < n; i++) {
    if (i - 1 == -1) {
        dp[i][0] = 0;
        // 解释：
        //   dp[i][0] 
        // = max(dp[-1][0], dp[-1][1] + prices[i])
        // = max(0, -infinity + prices[i]) = 0
        dp[i][1] = -prices[i];
        //解释：
        //   dp[i][1] 
        // = max(dp[-1][1], dp[-1][0] - prices[i])
        // = max(-infinity, 0 - prices[i]) 
        // = -prices[i]
        continue;
    }
    dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
}
return dp[n - 1][0];

空间优化：

// k == 1
int maxProfit_k_1(int[] prices) {
    int n = prices.length;
    // base case: dp[-1][0] = 0, dp[-1][1] = -infinity
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        // dp[i][1] = max(dp[i-1][1], -prices[i])
        dp_i_1 = Math.max(dp_i_1, -prices[i]);
    }
    return dp_i_0;
}

第二题，k = +infinity

如果 k 为正无穷，那么就可以认为 k 和 k - 1 是一样的。数组中的 k 已经不会改变了，也就是说不需要记录 k 这个状态了

int maxProfit_k_inf(int[] prices) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, temp - prices[i]);
    }
    return dp_i_0;
}

第三题，k = +infinity with cooldown

每次 sell 之后要等一天才能继续交易。只要把这个特点融入上一题的状态转移方程即可：

1
2
3

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
解释：第 i 天选择 buy 的时候，要从 i-2 的状态转移，而不是 i-1 。

int maxProfit_with_cool(int[] prices) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    int dp_pre_0 = 0; // 代表 dp[i-2][0]
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, dp_pre_0 - prices[i]);
        dp_pre_0 = temp;
    }
    return dp_i_0;
}

第四题，k = +infinity with fee

每次交易要支付手续费，只要把手续费从利润中减去即可。改写方程：

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee)
解释：相当于买入股票的价格升高了。
在第一个式子里减也是一样的，相当于卖出股票的价格减小了。

int maxProfit_with_fee(int[] prices, int fee) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, temp - prices[i] - fee);
    }
    return dp_i_0;
}

第五题，k = 2

1
2
3

原始的动态转移方程，没有可化简的地方
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

必须要对 k 进行穷举：

int max_k = 2;
int[][][] dp = new int[n][max_k + 1][2];
for (int i = 0; i < n; i++) {
    for (int k = max_k; k >= 1; k--) {
        if (i - 1 == -1) { /*处理 base case */ }
        dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
        dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
    }
}
// 穷举了 n × max_k × 2 个状态，正确。
return dp[n - 1][max_k][0];

这里 k 取值范围比较小，所以可以不用 for 循环，直接把 k = 1 和 2 的情况手动列举出来

dp[i][2][0] = max(dp[i-1][2][0], dp[i-1][2][1] + prices[i])
dp[i][2][1] = max(dp[i-1][2][1], dp[i-1][1][0] - prices[i])
dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], -prices[i])

int maxProfit_k_2(int[] prices) {
    int dp_i10 = 0, dp_i11 = Integer.MIN_VALUE;
    int dp_i20 = 0, dp_i21 = Integer.MIN_VALUE;
    for (int price : prices) {
        dp_i20 = Math.max(dp_i20, dp_i21 + price);
        dp_i21 = Math.max(dp_i21, dp_i10 - price);
        dp_i10 = Math.max(dp_i10, dp_i11 + price);
        dp_i11 = Math.max(dp_i11, -price);
    }
    return dp_i20;
}

第六题，k = any integer

有了上一题 k = 2 的铺垫，这题应该和上一题的第一个解法没啥区别。但是出现了一个超内存的错误，原来是传入的 k 值会非常大，dp 数组太大了。一次交易由买入和卖出构成，至少需要两天。所以说有效的限制 k 应该不超过 n/2，如果超过，就没有约束作用了，相当于 k = +infinity。这种情况是之前解决过的。

自此，跟股票划清界限了。